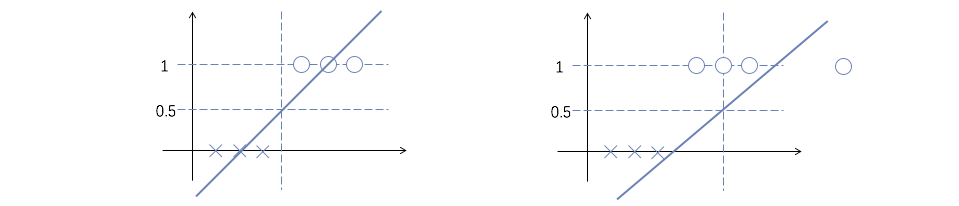
在二分类问题中，输出$y\in {0, 1}$。同样的，我们也可以用线性拟合来尝试解决二分类问题（如下图左），但数据点比较异常时，容易出现下图右这样的情况：

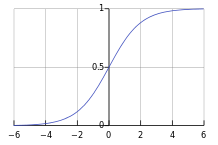
一般，在二分类问题中，我们会选用『logistic函数』来拟合（因为形状像S，又称为『sigmoid函数』）： $$ h_\theta (x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}} $$ logistic函数$g(z)=1/(1+e^{-z})​$的形状如下： 可以定义 $$ \begin{align} P(y=1|x;\theta)& =h_\theta (x) \\ P(y=0|x;\theta)& =1-h_\theta(x) \end{align} $$ 于是： $$ P(y|x;\theta)=h_\theta(x)^y(1-h_\theta(x))^{(1-y)} $$ 进行极大似然估计： $$ L(\theta)=P(y|x;\theta)=\prod_{i=1}^mP(y^{(i)}|x^{(i)};\theta)=\prod_{i=1}^mh_\theta(x^{(i)})^{y^{(i)}}(1-h_\theta(x^{(i)}))^{(1-y^{(i)})} $$ 为了计算方便，定义 $$ \begin{align} l(\theta)&=log(L(\theta))\\ &=\sum_{i=1}^mlog(P(y^{(i)}|x^{(i)};\theta))\\ &=\sum_{i=1}^m(y^{(i)}\cdot log(h_\theta(x^{(i)}))+(1-y^{(i)})\cdot log(1-h_\theta(x^{(i)}))) \end{align} $$ 利用梯度上升进行求解： $$ \theta := \theta + \alpha \nabla_\theta l(\theta) $$ 其中 $$ \nabla_{\theta_j} l(\theta)=\frac{\partial}{\partial\theta_j}l(\theta)=\sum_{i=1}^m(y^{(i)}-h_\theta(x^{(i)}))\cdot x_j^{(i)}\\ \theta_j:=\theta_j+\alpha \cdot \sum_{i=1}^m(y^{(i)}-h_\theta(x^{(i)}))\cdot x_j^{(i)} $$ 最终的梯度上升结果几乎与线性拟合中的梯度下降结果一样。